|
|
Measurement of 3D Eye Movements
|
|
|
|
 Download
Application
Note (PDF, 240 kB) Download
Application
Note (PDF, 240 kB)
|
|
|
|
|
Preliminary Note
|
|
This application note was originally written to describe the recording
of 3D eye (or head)
movements using our first generation search coil system Angle-Meter, which was introduced in 1989. Therefore, the given
performance data (noise, timing resolution etc.) within this application note is based on the output data of the Angle-Meter.
Please note that the performance of our
latest search coil system CS681 is dramatically increased compared to the
Angle-Meter. Read more about the
CS681...
|
|
|
|
|
|
|
Introduction
|
 |
|
|
|
|
|
Eye movements in 3D space are traditionally analyzed in terms of horizontal and vertical displacements of the line of sight and the rotation of the eye about the line of sight. Examples of these kinds of parameterizations of eye position are the coordinates introduced by Fick [1] and Helmholtz [2]. The output of the Angle-Meter is represented in a similar coordinate system. For describing the procedure of 3D eye (or head) movement recordings, we shall adopt a right-handed coordinate system and assume that the corresponding reference frames of the detector and the subject coincide in orientation.
|
|
|
|
[1] A. Fick, "Die Bewegungen des menschlichen Augapfels," Z. rationelle Med., vol. 4, pp. 101-128.
1977
[2] H. von Helmholtz, "Handbuch der Physiotogischen Oprik", Leipzig: Voss,
1986
|
|
|
|
|
|
|
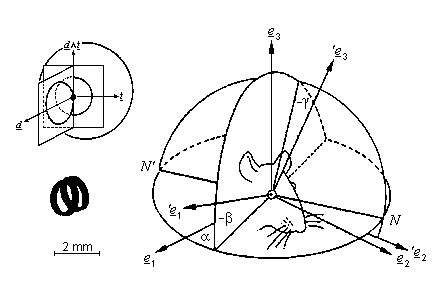
Figure 1
|
|
|
|

|
|
|
|
|
|
|
Technique
|
 |
|
|
|
|
The direction of line of sight is determined by two angles (Fig. 1): a horizontal angle alpha defining how far the eye (line of sight) is rotated about a vertical axis e3 and a vertical angle beta defining how far the eye is rotated about the nodal axis (axis N' N in Fig. 1 defined by the intersection of the plane through the center of rotation perpendicular to the new direction of the line of sight and the horizontal plane). Both angles can be measured simultaneously by a search coil, which is attached to the eye concentrically to the pupil (so-called direction coil). The rotation of the eye about the line of sight (ocular torsion) defines a third angle gamma as discussed below.
The outputs A (Azimuth) and B (Elevation) of the system are directly proportional to the angular displacements alpha and beta of the search coil relative to the system's reference frame. The channel gains GA and GB are independent of the geometrical and electrical characteristics of an individual search coil. The orientation of the coil area vector d with respect to the system's frame of reference is given by the angular parameters alpha (= output A / channel gain GA) and beta (= output B / channel gain GB) as follows:
|
|
|
|
(1)
|
|
Note that by the right-hand rule (i.e., downward movement positive), the component d3 is negative for a positive angle beta.
|
|
|
|
A complete description of the eye position in space requires recording of one more parameter that defines the state of rotation of the eyeball around the line of sight (ocular torsion). To this end, a second search coil (so-called torsion coil) must be attached to the eye in a non-parallel plane with respect to the first one (see the inset of Fig. 1). In such an arrangement, the outputs A1 and B1 (channel 1) and A2 and B2 (channel 2) define the angular orientation of coil 1 (i.e. direction coil with area vector d) and coil 2 (i.e. torsion coil with area vector t) in the system's reference frame. Given the fixed orientation of the two coils relative to each other, only three of the four parameters alpha1 (= output A1 / channel gain GA1), beta1 (= output B1 / channel gain GB1), alpha2 (= output A2 / channel gain GA2), and beta2 (= output B2 / channel gain GB2) are independent variables. The angle sigma between the coil area vectors d (direction coil) and t (torsional coil) is determined by the scalar product (note that d and t are unity vectors):
|
|
|

|
(2)
|
|
The parameters alpha1, alpha2, beta1 and beta2 are related to the angle gamma, which defines the amount of rotation (torsion) about an axis parallel to the direction coil axis as follows (for details, see
'Orthogonalization'):
|
|
|
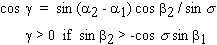
|
(3)
|
|
where sigma is the angle between the direction and the torsion coil area vector. Given the angle sigma, it is sufficient to measure the angles alpha1,beta1 and beta2 to determine the parameters alpha = alpha1, beta = beta1, and gamma, which provide a complete description of 3D eye positions.
|
|
|
|
Any eye position in head is given by a rotation:
|
|
|

|
|
|
where n is the normalized axis about which the eye has to rotate in order to go from a reference position to the current position, and rho is the angle of rotation about n. The product of two rotations R1R2 has the same vector
representation [1], [2]:
|
|
|

|
|
The rotation, bringing the eye from the reference position a = 0, b = 0, and g = 0 to the position defined by
angles a, b and g is given by the rotation vector:
|
|
|
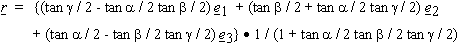
|
(4)
|
|
The orientation of the rotation axis is defined by n = r / ||r|| and the rotation angle by rho = 2 tan-1 (||r||) where || || denotes the norm of a vector.
|
|
|
|
Examples of 3D eye movement records obtained from head-restrained rats with the Angle-Meter are illustrated in Figs. 2 and 3. The eye movements were recorded with a dual search coil consisting of two miniature coils (80 turns, diameter 2 mm, weight 1.1 mg) that were glued on top of each other in approximately perpendicular planes (see the inset of Fig. 1). The assembly was attached concentrically to the pupil onto the anaesthetized cornea of the right eye using a tiny drop of a histocompatible glue. The dual search coil was oriented on the eye such that one coil was plane on the cornea approximately aligned with the optic axis of the eye (direction coil) and the other coil approximately in a vertical plane (torsion coil) (for further details, see [3]).
|
|
|

|
|
|
|

|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
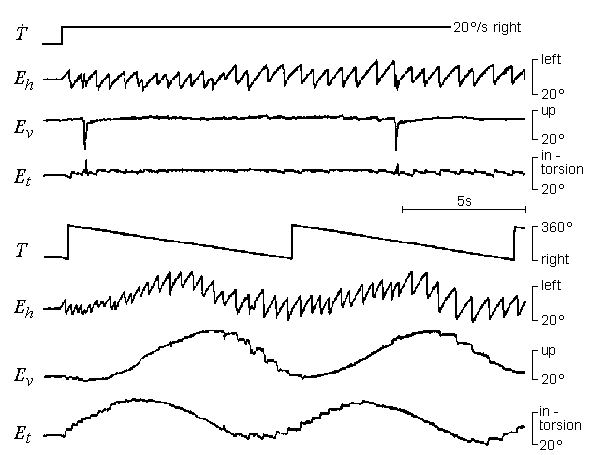
Saccadic eye movements in the rat are often confined to the horizontal plane (Eh = output A1 of Fig. 2) showing only minor vertical (Ev = output B1 of Fig. 2) and torsional (Et = output B2 of Fig. 2) components. In order to obtain the true ocular torsion, the output B2 must be corrected off line according to the above outlined procedure. In the illustrated case the direction coil (optic axis of the eye) was directed upwards by about 20°, resulting in an increased quantal noise of about 0.5° peak to peak in the horizontal trace Eh. The maximal useful time resolution of the recording is 5 ms. It is determined by the sampling rate of the Angle-Meter of 400 Hz.
|
|
|
|
When rotating an animal on a turntable about a vertical axis in front of a structured visual background, a horizontal nystagmus was elicited (upper panel of Fig. 3). Only minor vertical and torsional eye movement components were present. In contrast, horizontal, vertical, and torsional eye movements were elicited by rotating the animal about its vertical axis on a tilted platform (lower panel of Fig. 3). As mentioned above, the torsional movement components Et have to be corrected off line by taking into account vertical eye position as well as a possible deviation from space quadrature of the dual search coil (see (7)). With the corrected torsion component at hand, the instantaneous orientation of the rotation axis of the eye in space can be calculated as outlined above.
|
|
|
|
[1] W. Haustein, "Considerations on Listing's law and the primary position ..." Biol. Cybern., vol. 60, pp. 411-420, 1989
[2] K. Hepp, "On Listing's law," Comm. Math. Phys., vol. 132, pp. 285-292, 1990
[3] B. J. M. Hess and N. Dieringer, "Spatial organization of the maculo-ocular ..." Euro. J. Neurosci., vol. 2, pp. 909-919, 1990
|
|
|
|
|
|
Orthogonalization
|
 |
|
|
|
|
|
In order to measure eye position in 3D space [1], two search coils, arranged in nonparallel planes, must be used. We shall assume that one coil with area vector d is attached in the frontal plane (direction coil) and another one with coil vector t (torsion coil) in a nonfrontal plane of the eye (or head). For simplicity, we shall also assume that the direction coil vector points along the line of sight and that the vectors d, t and d ^ t establish a right-handed reference system. To calculate the torsion around the line of sight, we first have to determine the orthogonal complement of the vector t with respect to the vector d:
|
|
|
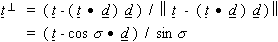
|
(5)
|
|
Given the output voltages A1, B1, A2 and B2, the angle sigma between the two coils is obtained with the help of (2). As to the torsion angle of the search coil with respect to the orientation of the direction coil, we refer to the plane determined by the axes ex and ey of the reference frame of the system. For a given position of the search coil, we define a reference torsion vector
|
|
|
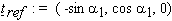
|
(6)
|
|
such that d . tref = 0. The torsion angle gamma with respect to the reference torsion vector is given by
|
|
|
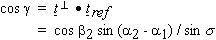
|
(7)
|
|
|
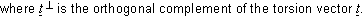
|
|
|
|
|
This relation defines the magnitude of the torsion angle gamma. The sign of the torsion is obtained from the cross vector product
|
|
|
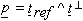
|
(7')
|
|
|
|
A torsion is positive if the first component of the vector p is pointing along d - d3e3. This means that
|
|
|
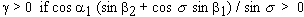
|
(8)
|
|
|
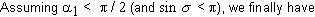
|
|
|
|
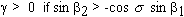
|
(8')
|
|
|
|
[1] H. Kasper and B. J. M. Hess, "Magnetic search coil ..." IEEE Trans. Biomed. Eng., vol. 38, no. 5, pp. 466-475, 1991
|